平成28年度神奈川県公立高校入試〈英語〉乱択での得点期待値

平成28年度神奈川県公立高校入試問題〈英語〉における、乱択での得点期待値は「13.72点」です。

まったく知識のない受験生があてずっぽうで（＝乱択で）選択問題だけを解いた場合の得点期待値を計算しました。

それぞれの問題の配点に「当たる確率」（４択問題であれば、「４分の１」）を掛け合わせた値を合算しています。

神奈川県公立高校入試2016 英語

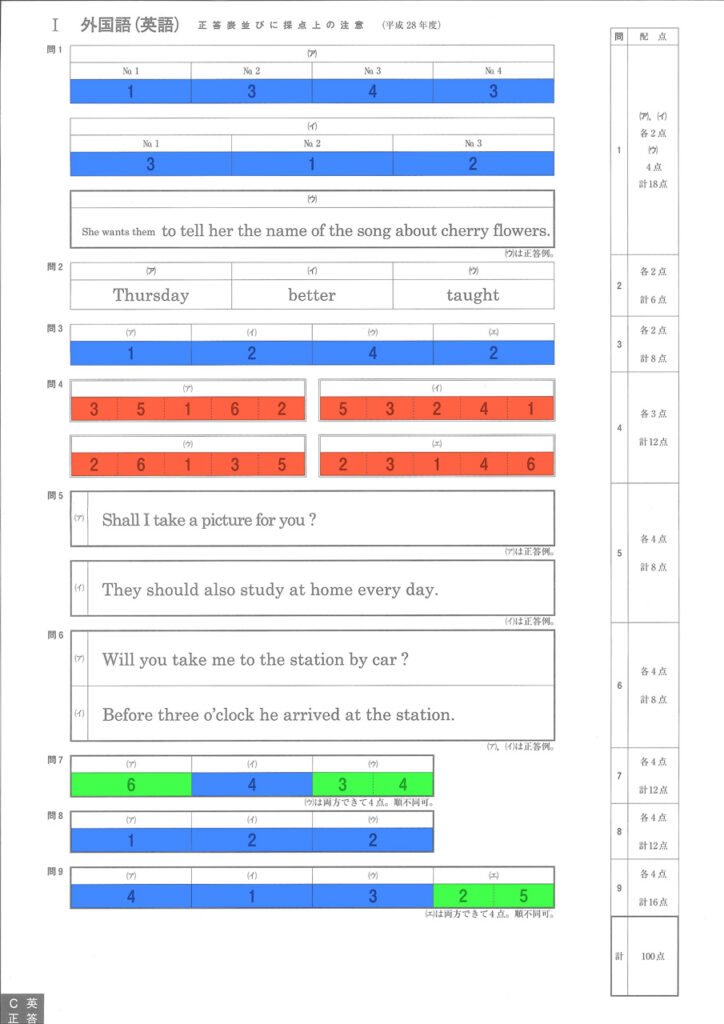
平成28年度神奈川県公立高校入試英語得点期待値

４択問題（上図中の青い部分）は全部で18問ありました。

配点は、

です。

ここから、４択問題での得点の期待値は「12.5点」となります。

{(2×1/4)x11}＋{(4×1/4)×7}=5.5＋7=12.5

問４（上図中の赤い部分）は、「六つの語の中から五つを選んで正しい順番に並べかえ」る問題です。配点はすべて３点です。

この問題形式では、解答パターンが全部で 6×5×4×3×2=720 通りありますので、それぞれの小問の「当たる確率」は「720分の１」となります。

ここから、問４全体での得点の期待値は「60分の１点」です。

(3×1/720)×4=1/60

その他の選択問題（上図中の緑色の部分）です。

問７の（ア）の配点は４点です。６択問題なので、「当たる確率」は「６分の１」です。得点の期待値は「６分の４点」です。
問７の（ウ）と問９の（エ）は６つの選択肢から２つを選ぶ問題です。２つが「両方できて４点。順不同可」です。解答パターンは全部で15通りありますので、「当たる確率」は「15分の１」となります。得点の期待値は、問７と問９を合わせて「15分の８点」です。